Natuurkunde

Table of contents

Elektriciteit

Basisbegrippen

Lading

Elektriciteit bestaat uit positief en negatief geladen deeltjes die bewegen. Geladen deeltjes met tegengestelde ladingen trekken elkaar aan. Deeltjes met gelijke ladingen stoten elkaar af.

Lading (\(Q\)) meten we in Coulomb (C).

Stroomkring

Een stof geleidt stroom als er geladen deeltjes vrij kunnen bewegen. In metalen zijn dit de vrije elektronen (in het metaalrooster), maar in sommige (zout-)oplossingen zijn het ionen.

Als er een gesloten stroomkring met spanningsbron is, lopen er elektronen van de min- naar pluspool. Dat begrepen natuurkundigen eerst niet, dus we hebben afgesproken dat de lading van min naar plus beweegt, maar de stroom van plus naar min (andersom).

Stroomsterkte

De stroomsterkte (\(I\)) is een maat voor de hoeveelheid lading die per tijdseenheid door een punt in de stroomkring loopt. Eigenlijk gewoon het aantal elektronen dat langskomt.

We meten dit in Ampère (A), gelijk aan Coulomb per seconde (C/s).

\[I = Q/t\]

Een stroommeter plaats je altijd in de stroomkring, tussen de andere componenten:

Capaciteit

We gebruiken de eenheid Ampère-uur (Ah) soms als alternatief voor Coulomb om de capaciteit van een batterij aan te geven. De capaciteit van een batterij is de maximale hoeveelheid lading die hij kan leveren.

De Ampère-uur geeft de hoeveelheid lading aan die in één uur bij \(1 \text{A}\) stroomt:

\[1 \text{ Ah} = 1 \text{ A} \cdot 3600 \text{ s} = 3.6 \cdot 10^3 \text{ C}\]

Spanning

De spanning (\(U\)) is de hoeveelheid energie die de lading (in dit geval elektronen) meedraagt. Je meet dit door het energieverschil tussen twee punten te vergelijken.

We meten spanning in Volt (V), wat gelijk is aan Joule per Coulomb (J/C).

\[U = \Delta E / Q\]

Een spanningsmeter staat daarom altijd buiten de stroomkring. Je meet hiermee de spanning over een aantal componenten:

Vermogen

Elektrische schakelingen zetten elektrische energie om in andere soorten energie. De hoeveelheid energie die per seconde wordt omgezet (aka het energieverbruik) noemen we het vermogen (\(P\)).

We meten het vermogen in Watt (W), wat gelijk is aan Joule per seconde (J/s).

\[P = E/t\]

Je kan het vermogen ook berekenen door de stroomsterkte en spanning te vermenigvuldigen:

\[P = U \cdot I = \frac{E}{Q} \cdot \frac{Q}{t} = E/t\]

Weerstand

De weerstand (\(R\)) van een stof geeft aan hoe goed deze stroom geleidt; een hoge weerstand zorgt voor een lage stroomsterkte. We meten weerstand in Ohm (\(\Omega\)).

De weerstand van een materiaal wordt voornamelijk bepaald door het soort stof (de soortelijke weerstand, \(\rho\)). Ook temperatuur speelt een rol: sommige materialen geleiden bij verhitting beter (NTCs), andere juist slechter (PTCs).

Als een materiaal ongeacht de temperatuur een constante weerstand heeft, noemen we dat een Ohmse weerstand. Daarvoor geldt:

\[R = U/I\]

Bij een Ohmse weerstand is het U,I-diagram dus een rechte lijn door de oorsprong.

Weerstand van een draad

\[R = \rho \frac{l}{A} \text{ met } A = \frac{1}{4} \pi d^2\]

Je ziet in de formule geen \(T\), omdat het effect van de temperatuur op de weerstand per materiaal verschilt. Dit is meegenomen in de soortelijke weerstand (\(\rho\)). Let dus wel op dat je de soortelijke weerstand bij de juiste temperatuur neemt.

Halfgeleiders

Halfgeleiders zijn materialen die uit zichzelf weinig vrije elektronen hebben en daardoor slecht geleiden, maar waarbij onder bepaalde omstandigheden meer elektronen vrijkomen en dan dus wel goed geleiden.

Schuifweerstand

Als variabele weerstand

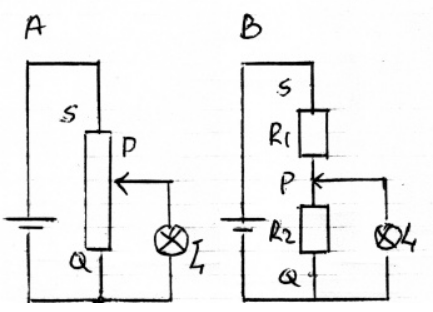
Met een schuifweerstand kan je zelf de weerstand van de weerstand bepalen (lol). Alleen door het stuk tussen de pijl en de uitgang van de schuifweerstand loopt stroom.

Door de schuifweerstand kleiner te maken wordt de weerstand dus lager.

Als spanningsdeler

Als je een schuifweerstand als spanningsdeler gebruikt gebruik je alle drie de aansluitpunten. Daarmee komt een deel van de weerstand in parallel te staan.

…

Schakelingen

Serieschakeling

In een serieschakelijk is er sprake van spanningsdeling; de stroomsterkte door de gehele schakeling constant:

\[U_{tot} = U_1 + U_2 + … U_n\] \[I_{tot} = I_1 = I_2 = … I_n\] \[R_{tot} = R_1 + R_2 + … R_n\]

Parallelschakeling

In een parallelschakelijk is sprake van stroomdeling; de spanning is door alle vertakking constant:

\[I_{tot} = I_1 + I_2 + … I_n\] \[U_{tot} = U_1 = U_2 = … U_n\] \[\frac{1}{R_{tot}} = \frac{1}{R_1} + \frac{1}{R_2} + … \frac{1}{R_n}\]

Mechanica

Basisbegrippen

Arbeid

Arbeid (\(W\)) is de energie die verbruikt wordt bij het uitoefenen van een kracht over afstand. We meten dit in Newtonmeter (Nm), wat gelijk is aan Joule (J).

\[W = Fs\]

Mechanische energie

Mechanische energie (\(E_m\)) is de som van de kinetische energie en zwaarte-energie:

\[E_m = E_{kin} + E_z\]

Vermogen

Vermogen (\(P\)) is de hoeveelheid arbeid die verricht wordt per seconde:

\[P = W/t = Fs/t = Fv\]

Verbrandingswarmte

De verbrandingswarmte (\(r_v\)) is de hoeveelheid (chemische) energie die vrijkomt bij het verbranden van een volume van een brandstof.

We meten verbrandingswarmte in J/kg (voor vaste stoffen), J/m3 (voor gassen) of J/L (voor vloeistoffen).

\[E_{chem} = r_v V \text{ of } E_{chem} = r_v m\]

Krachten

Krachten (\(F\)) zijn een vector-eenheid. Dat betekent dat ze precies werken zoals vectoren bij wiskunde. Elke kracht heeft drie eigenschappen:

Aangrijpingspunt Bij wiskunde mag je het aangrijpingspunt van een vector vrij bewegen. Bij krachten mag je het aangrijpingspunt alleen verschuiven langs de lijn van de richting waarin de kracht werkt.

De resulterende (of netto) kracht (\(F_{res}\)) is de som van alle krachten die op een voorwerp werken.

Wetten van Newton

  1. Als de resulterende kracht op een voorwerp nul is, is het in rust of beweegt het met een constante snelheid langs een rechte lijn.

  2. \(F_{res} = ma\)

  3. Krachten zijn een wisselwerking. Als een voorwerp een actiekracht uitoefenent op een ander voorwerp, zal dat voorwerp reageren met een reactiekracht die even groot en tegengesteld is.

Soorten

Maximale schuifwrijvingskracht

De schuifweerstandskracht is een reactiekracht op de actiekracht die een voorwerp verschuift. Tot op de maximumwaarde (\(F_{w,s,max}\)) is deze gelijk en tegengesteld aan de actiekracht. Vanaf de maximumwaarde blijft hij constant:

\[F_{w,s} = F_{\text{actie}} \text{ mits } F_{\text{actie}} < F_{w,s,max}\]

Dat is waarom een boek niet verschuif als je er maar een beetje tegen duwt, maar het wel verschuift als je harder duwt.

Middelpuntzoekende kracht

De middelpuntzoekende kracht \(F_{mpz}\) is geen losse kracht, maar een rol die één of meer krachten kunnen vervullen, net als hoe de resulterende kracht geen echte kracht is, maar een rol die door verschillende krachten samen vervuld wordt.

De middelpuntzoekende kracht is een kracht die loodrecht op de bewegingsrichting staat:

\[F_{mpz} = \frac{mv^2}{r}\]

Door de middelpuntzoekende kracht is er een versnelling loodrecht op de snelheid. Daardoor verandert de grootte van de snelheid niet, maar de bewegingsrichting wel.

Energie

Wet van behoud van energie

Volgens de wet van behoud van energie kan er geen energie ontstaan of afgebroken worden; het kan alleen van vorm veranderen. De som van alle energie aan het begin is dus gelijk aan de som van de energie op het eind:

\[\Sigma E_{\text{begin}} = \Sigma E_{\text{eind}}\]

De hoofdletter sigma (\(\Sigma\)) is een opsommingsteken. Hier staat dus: alle energie aan het begin is gelijk aan alle energie aan het eind.

Soorten

Let op! De bovenstaande formule voor veerenergie geldt alleen bij een ideale veer.

Nulpunt van de gravitatie-energie

Bij de meeste energiesoorten mag je zelf bepalen waar het nulpunt ligt. Bij gravitatie-energie hebben we afgesproken dat het nulpunt op oneindig grote afstand ligt.

Zolang iets gravitatiekracht ondervindt van een massa, kan het zich niet volledig vrij bewegen. We hebben daarom afgesproken dat het nulpunt van de gravitatie-energie ligt op het punt dat je buiten bereik van de andere massa bent, op \(r = \infty\).

De gravitatie-energie is dus altijd negatief, maar naarmate hij groter wordt nadert hij nul (wordt minder negatief).

Nulpunt van de elektrische energie

Elektrische energie volgt een vergelijkbare conventie naar gravitatie-energie.

Zolang een elektron zich in een atoom bevindt, ondervindt het elektrische kracht en kan het zich dus niet vrij bewegen. Daarom hebben we, net als bij gravitatiekracht, afgesproken dat het nulpunt van de elektrische energie ligt waar het elektron geen aantrekking van de atoomkern meer heeft.

De elektrische energie is dus binnen een atoom negatief, en daarbuiten positief.

Bewegingen

Afstand (\(s\)) is de totale afstand die een object heeft afgelegd. Plaats (\(x\)) is de netto afgelegde afstand. In veel situaties zijn ze uitwisselbaar.

Snelheid (\(v\)) is verandering van plaats (\(x’\)) en versnelling (\(a\)) is verandering van snelheid (\(x’’\)).

De momentale snelheid of versnelling (aka op een bepaald tijdstip) bepaal je aan de hand van een raaklijn. De gemiddelde snelheid (\(v_{gem}\)) en gemiddelde versnelling (\(a_{gem}\)) bereken je met:

\[v_{gem} = \frac{\Delta x}{\Delta t} \text{ } \text{ en } \text{ } a_{gem} = \frac{\Delta v}{\Delta t}\]

In een eenparige beweging is de snelheid constant, dus is de gemiddelde snelheid gelijk aan de momentale snelheid op elk tijdstip.

Cirkelbewegingen

In een (eenparige) cirkelbeweging kan je aan de hand van de straal (\(r\)) en omlooptijd (\(T\)) de snelheid bepalen:

\[v = \frac{\Delta x}{\Delta t} = \frac{2\pi r}{T}\]

De omlooptijd is de tijd die nodig is voor één rondje.

Astrofysica

Zonnestelsel

Wetten van Kepler

  1. Planeten beschrijven een ellipsbaan met de ster in één van de brandpunten.
  2. Planeten hebben een grotere snelheid als ze dichter bij de ster zijn.
  3. \(\frac{r^3}{T^2} = \frac{GM}{4\pi^2}\)

\(M\) is de som van de massa van de ster en planeet. In veel gevallen is de massa van de planeet verwaarloosbaar klein tenopzichte van de massa van de ster.

Gravitatiekracht

Gravitatiekracht is een wisselwerking tussen twee massa’s. De gravitatiekracht werkt op afstand en is omgekeerd evenredig met de straal tussen de massa’s. Het aangrijpingspunt van de kracht is het zwaartepunt van de massa; bij een bol is dat het middenpunt.

Ontsnappingssnelheid

De ontsnappingssnelheid is de minimaal benodigde snelheid om volledig aan de gravitatiekracht van een hemellichaam te ontsnappen. De formule is herleidt aan de hand van de gravitatie-energie:

\[E_{kin,0} + E_{g,0} = E_{kin,\infty} + E_{g,\infty}\] \[E_{kin,0} + E_{g,0} = 0 \implies v_0 = \sqrt{\frac{2GM}{r^2}}\]

Satellietbanen

Geostationaire baan

Een geostationaire baan is een satellietbaan waarbij de satelliet op één vast punt boven het aardvlak meebeweegt. Dan:

Vanwege deze voorwaarden is een geostationaire baan alleen mogelijk op één hele specifieke hoogte en snelheid, boven de evenaar.

Derde wet van Kepler

De derde wet van Kepler geldt ook voor satellietbanen rond de aarde. Hiermee kan je de hoogte en baansnelheid berekenen:

\[r = \sqrt[3]{\frac{GM_{aarde} \cdot T^2}{4\pi^2}} = 42 \cdot 10^6 \text{ m}\]\[h = r - R_{aarde} = 35.7 \cdot 10^3 \text{ km}\]\[v = \frac{2\pi r}{T} = 3.1 \text{ m/s}\]

Polaire baan

Een polaire baan is een relatief lage satellietbaan waarbij een satelliet in 1 à 2 uur over beide polen vliegt. Omdat de aarde zelf ook draait “ziet” de satelliet op den duur dus elk stukje aarde.

Stralings- & planckkrommen

De fotosfeer (buitenste laag van een ster) zendt EM-straling uit. Niet van elke frequentie wordt evenveel straling uitgezonden. In een stralingskromme kan je voor elke golflengte (\(\lambda\)) de stralingsintensiteit (\(I\)) zien:

De oppervlakte onder de grafiek is de totale stralingsintensiteit.

De oppervlaktetemperatuur (aka effectieve temperatuur) kan je vinden aan de hand van de kleur van een ster. De kleur wordt bepaald door het stralingsmaximum (de piek in de grafiek). Hoe warmer de ster, hoe meer blauw licht hij uitzendt, hoe verder de piek naar links ligt.

De exacte temperatuur bepaal je door een planckkromme te vinden die past bij je stralingskromme. Een planckkromme is de stralingskromme die een ster met een bepaalde oppervlaktetemperatuur theoretisch gezien zou moeten hebben.

Dus: stel dat de piek van de experimenteel bepaalde stralingskromme ligt op ~500 nm, zoek je een planckkromme in Binas 22A met een piek op ook ~500nm, en lees je de temperatuur af (in dit geval ~5700K).

Voor de planckkrommen geldt de wet van Wien:
(Hoe warmer, hoe lager de \(\lambda_{max}\), hoe blauwer, hoe verder de piek naar links.)

\[\lambda_{max} = \frac{K_W}{T_{eff}}\]

\(k_W\) staat in Binas 7A

Sterren

Vermogen & intensiteit

Het stralingsvermogen (\(P\)) is de hoeveelheid stralingsenergie die een ster per seconde uitzendt. Dit hangt af van de oppervlakte en temperatuur van de ster:

\[P = \sigma A T_{eff}^4\]

De stralingsintensiteit (\(I\)) is de ontvangen stralingsenergie die wij per vierkante meter kunnen waarnemen op het aardoppervlak. Deze neemt kwadratisch af met de afstand tot de ster (\(r\)):

\[I = \frac{P_{\text{bron}}}{4\pi r^2}\]

HDR

In een HDR-diagram word de lichtkracht (\(L\)) van een ster uitgezet tegen zijn effectieve temperatuur (\(T_{eff}\)). De lichtkracht is het vermogen van een ster tenopzicht van de zon:

\[L = \frac{P}{P_{\text{zon}}}\]

In het HDR liggen de sterren op verticale assen (‘reeksen’), die de straal van tenopzicht van de zon (\(R\)) aangeven.

Aan de hand van de oppervlaktetemperatuur en reeks (er mag uitgegaan worden van de hoofdreeks als dit niet expliciet gespecificeerd wordt), kan het stralingsvermogen van de ster bepaald worden:

\[P = P_{\text{zon}} \cdot 10^n\]

waarbij \(n\) de afgelezen waarde is op \(\log(T_{eff})\)

Als de stralingsintensiteit op aarde (\(I\)) bekend is, kan je ook de afstand tot de ster (\(r\)) bepalen:

\[r = \sqrt{\frac{4 \pi \cdot I}{P}}\]

Spectraalanalyse

Een spectrum (zoals stralingskrommen) laat zien welke golflengtes er in straling voorkomen.


Een gloeidraad of ster zend normaliter een continuspectrum uit, waarin alle kleuren (golflengtes) voorkomen.


In een koud gas bevinden de elektronen zich in een lage energietoestand. Door het absorberen van fotonen ‘springen’ ze naar een hoger energieniveau. Dit gebeurt alleen als \(E_f = \Delta E\); daardoor worden maar enkele golflengtes fotonen geabsorbeerd.


In een heet gas bevinden elektronen zich in een verhogde energietoestand. Sporadisch zullen elektronen terugvallen naar een lager energieniveau. Daarbij wordt een foton uitgezonden waarbij weer geldt \(E_f = \Delta E\). Dit veroorzaakt de emissielijnen in het emissiespectrum.

De energieniveaus verschillen per atoomsoort, dus de golflengtes die worden uitgezonden hangen af van de samenstelling van het gasmengsel.

Doppler-verschuiving & radiale snelheid

Als sterren bewegen worden de golven van de EM-straling samengedrukt of uitgerekt door het Dopler-effect. Daardoor worden de golflengtes groter of kleiner.

Sterren draaien om hun as. De snelheid waarmee ze dit doen noem je de radiale snelheid. Door de draaing beweegt de ene kant van de ster van ons af, en de andere kant naar ons toe. Daardoor is er zowel een rood- als blauwverschuiving, en wordt de emissielijn in het spectrum breder.

Het verschil tussen de hoogste en laagste golflengte van een balk in het spectrum is \(\Delta \lambda\). Hiermee kan je de radiale snelheid berekenen:

\[v_r = c \cdot \frac{\Delta \lambda}{\lambda}\]

Golven

Trillingen

Een trilling is de periodieke beweging van een voorwerp. Daarbij spreken we van een veranderende uitwijking ten opzichte van een evenwichtsstand.

Een trilling heeft een aantal eigenschappen:

De frequentie is het aantal periodes per seconde, dus omgekeerd evenredig met de trillingstijd:

\[f = 1 / T\]

Een harmonische trilling is een een trilling waarvan de uitwijking als een sinusoïde kan worden beschreven. Dit kan alleen als de trilling een vaste amplitude en trillingstijd heeft. De uitwijking (\(u\)) van een harmonische trilling op tijdstip (\(t\)) drukken we uit als:

\[u(t) = A \cdot \sin(\frac{2\pi}{T} \cdot t)\]

De bewegingssnelheid van een trillend punt is maximaal in de evenwichtsstand. Die snelheid berekenen we aan de hand van:

\[v_{max} = \frac{2\pi A}{T}\]

Interferentie

Superpositie (of interferentie) is het optellen van (de uitwijking van) trillingen.

Voorbeeld Stel je hebt twee geluidsgolven die elkaar kruisen met één een overdruk van 4 en de ander een onderdruk van 1, dan wordt de uiteindelijke druk dus een overdruk van 3.

Resonantie is een vorm van constructieve interferentie, waarbij de eigenfrequentie van een voorwerp versterkt wordt.

Interferentiepatroon

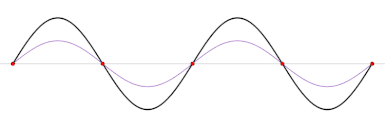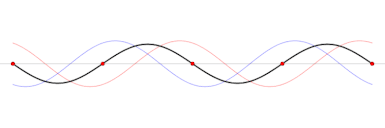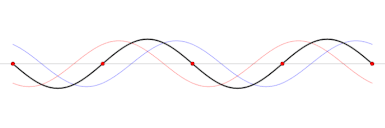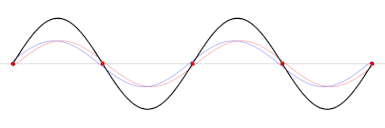
De interferentie van twee coherente (gelijke frequentie en constant faseverschil) puntbronnen vormt een patroon van buiklijnen met maximale versterking en knooplijnen met volledige uitdoving.

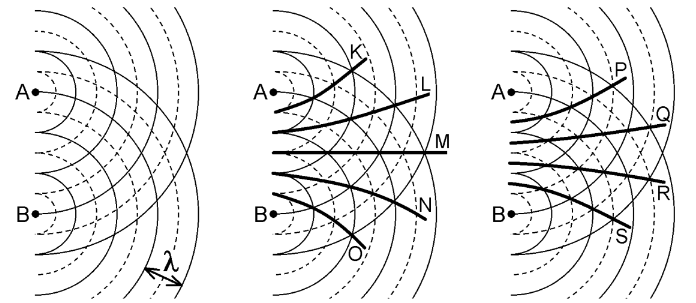
In de bovenstaande afbeelding zijn de doorgetrokken lijnen de toppen, en de gestippelde lijnen de dalen. Het tweede plaatje geeft maximale versterking aan (de buiklijnen), en het derde plaatje volledige uitdoving (de knooplijnen).

Het weglengteverschil is het afstandsverschil van een willekeurig punt to beide bronnen. Op buiklijnen geldt \(s_{weglente} = n\lambda\) en op knooplijnen geldt \(s_{weglente} = (n + \frac{1}{2}) \lambda\).

Het maximaal aantal buiklijnen is gelijk aan het aantal golflengtes afstand tussen de bronnen. Meer maxima zorgen voor een minder scherp interferentiepatroon. Dit gebeurt dus als de afstand tussen de bronnen toeneemt of de golflengte kleiner wordt.

Als je de puntbronnen naar elkaar toe beweegt divergeren de buik- en knooplijnen. Als je ze van elkaar af beweegt convergeren ze juist.

Lopende golf

Een golf is de voortplanting van een trilling door een medium. Dit kan op twee manieren:

Voorbeeld

De golflengte (\(\lambda\)) is de afstand die een golf aflegt in één trillingstijd. Samen met de frequentie bepaalt dit de golfsnelheid (\(v\)): de snelheid waarmee een golf zich voortplant.

\[v_{golf} = \lambda f\]

Voor geluid in lucht is dit \(434 \text{ m/s}\).
Trillingssnelheid en golfsnelheid

Let op: in een transversale golf zijn er dus twee soorten bewegingen. De individuele trillende punten gaan op en neer, en de gehele trilling plant zich daar loodrecht op voort.

De maximale trillingssnelheid van een trillend punt (\(v_{max}\)) is dus niet hetzelfde als de golfsnelheid (\(v_{golf}\)), omdat dit twee verschillende (loodrechte) bewegingen zijn.

Staande golf

Twee lopende golven met gelijke amplitude en frequentie kunnen tegen elkaar in lopen en dan zo met elkaar interfereren dat er op vaste punten maximale versterking en volledige uitdoving ontstaat.

We noemen dit staande golven (de maxima bewegen niet meer, dus de golf “staat stil”). De maxima noemen we buiken en de nulpunten noemen we knopen.

De afstand tussen twee buiken of knopen is \(\frac{1}{2}\lambda\), dus de afstand tussen een buik en een knoop is \(\frac{1}{4}\lambda\).

Grondtoon & boventonen

In buizen en snaren treedt bij de juiste lengte resonantie op, waardoor er staande golven onstaan. Een staande golf is een buis heeft altijd een buik bij de opening, en een knoop bij een gesloten uiteinde. Bij een snaar zijn beide uiteindes knopen

De grondtoon is de toon met de minimale hoeveelheid knopen en buiken:

-----------          |----------          |-----------|
 B   K   B     en    | K      B     en    | K   B   K |
-----------          |----------          |-----------|

Er kunnen oneindig veel boventonen bij komen. Dan komt er steeds een buik en een knoop bij:

-----------          |----------          |-----------|
 B K B K B     en    | K B K B      en    | K B K B K |
-----------          |----------          |-----------|

De lengte (\(l\)) van een open buis is \(\frac{1}{2}\lambda_1\) (van de grondtoon), omdat er twee buiken zijn. Voor een gesloten buis is er een buik minder, dus geldt \(l = \frac{1}{4}\lambda_1\).

\[l = n \cdot \frac{1}{2}\lambda_n \text{ voor open buizen, en:}\] \[l = n \cdot \frac{1}{2}\lambda_n - \frac{1}{4} \lambda_n \text{ voor gesloten buizen}\]

Waarin \(n = 1\) voor de grondtoon, \(n = 2\) voor de eerste boventoon enzovoort.
Verhoudingen

\(\lambda_1 : \lambda_2 : \lambda_3 : \lambda_4 = \frac{1}{2} : \frac{2}{2} : \frac{3}{2} : \frac{4}{2}\) voor open buizen
\(\lambda_1 : \lambda_2 : \lambda_3 : \lambda_4 = \frac{1}{4} : \frac{3}{4} : \frac{5}{4} : \frac{7}{4}\) voor gesloten buizen

De frequentie is omgekeerd evenredig met de golflengte (want \(f = v / \lambda\)), dus daaruit volgt de verhouding:

\(f_1 : f_2 : f_3 : f_4 = 1 : 2 : 3 : 4\) voor open buizen
\(f_1 : f_2 : f_3 : f_4 = 1 : 3 : 5 : 7\) voor gesloten buizen

Fase

De fase (\(\varphi\)) van een golf of trilling is het aantal afgelegde perioden of golflengten sinds het beginpunt van de golf of trilling.

De gereduceerde fase (\(\varphi_{red}\)) is de fase vanaf het begin van de huidige trilling. Je telt dus alle volledige trillingen niet mee:

Het (gereduceerde) faseverschil (\(\Delta \varphi\)) is het verschil in fase tussen twee trillingen of golven.

\[\Delta \varphi = \frac{\Delta t}{t}\] \[\Delta \varphi = \frac{\Delta x}{\lambda}\]

In fase en tegenfase

Als \(\varphi_{red} = 0\) zijn trillingen in fase. Bij optellen is er dan sprake van constructieve interferentie. Als \(\varphi_{red} = \frac{1}{2}\), zijn de golven in tegenfase. Bij superpositie treedt er dan juist destructieve interferentie op.

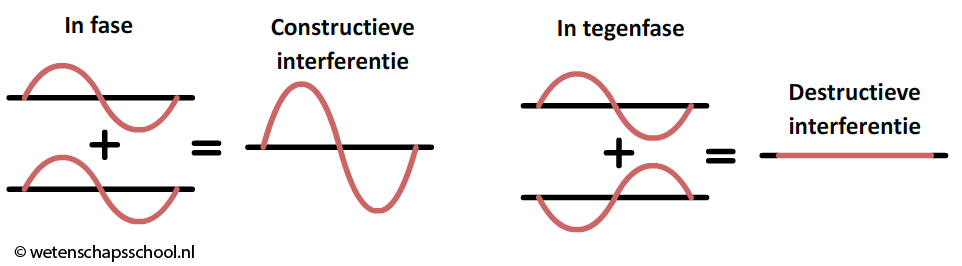
Bij elk ander (gereduceerd) faseverschil is er afwisselend sprake van versterking en uitdoving. Dat noemen we zwevingen.

Diagrammen

u,t-diagram (oscillogram)

Een oscillogram is een grafiek van een trilling. Het is een diagram waarmee de uitwijking van één trillend punt door de tijd wordt beschreven.

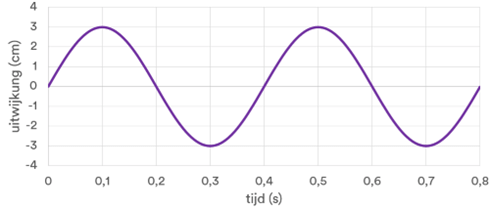
u,x-diagram

Een u,x-diagram is een grafiek van een golf. Het is een diagram waarmee je de uitwijking van de uitwijking van alle punten op één specifiek tijdstip af te lezen is.

Niet door elkaar halen Dus: een u,t-diagram laat zien hoe één punt op en neer beweegt door de tijd, terwijl een u,x-diagram laat zien waar alle punten zich op één specifiek tijdstip bevinden.

Geluid

Bij geluid noemen we amplitude volume en frequentie toonhoogte. De golfsnelheid van geluidsgolven noemen we de geluidssnelheid. In lucht is dit \(434 \text{m/s}\).

Een harmonische trilling wordt ook een zuivere toon genoemd. De superpositie van één of meer (zuivere) tonen geeft een samengestelde toon:

Zuivere toon Samengestelde toon

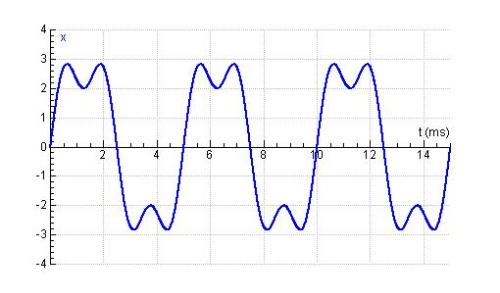De frequentie van een samengestelde toon wordt bepaald door de frequentie van de laagste toon die erin voorkomt, wat je de grondtoon noemt.

Kernfysica

Radioactiviteit

Radioactieve stoffen zijn isotopen waarvan de kernen instabiel zijn door een overschot of tekort aan neutronen. Die kernen kunnen uit elkaar vallen en zenden daarbij straling uit.

Radioactieve straling is een vorm van ioniserende straling. Deze straling is schadelijk voor mensen omdat het de atomen waaruit onze cellen bestaan kan ioniseren.

Omdat de kernen uit elkaar vallen, blijft er steeds minder van de radioactieve stof over. Na de halveringstijd (\(t_{1/2}\)) is de helft van de kernen uit elkaar gevallen.

Het aantal vervallen kernen per seconde noemen we de activiteit (\(A\)) in Becquerel (Bq). Die kan je voor een bepaald tijdstip (\(t\)) uitrekenen:

\[A = A_0 \cdot (\frac{1}{2})^{t/t_{1/2}}\]

De activiteit neemt na verloop van tijd af, omdat er steeds minder kernen overblijven (en dus ook minder kernen tegelijk kunnen vervallen). Het aantal overgebleven kernen op tijdstip (\(t\)) bereken je zo:

\[N = N_0 \cdot (\frac{1}{2})^{t/t_{1/2}}\]

Omrekenen naar massa Je kan het aantal kernen omrekenen naar massa door te vermenigvuldigen met de atoommassa van het betreffende isotoop.

Vervalkromme

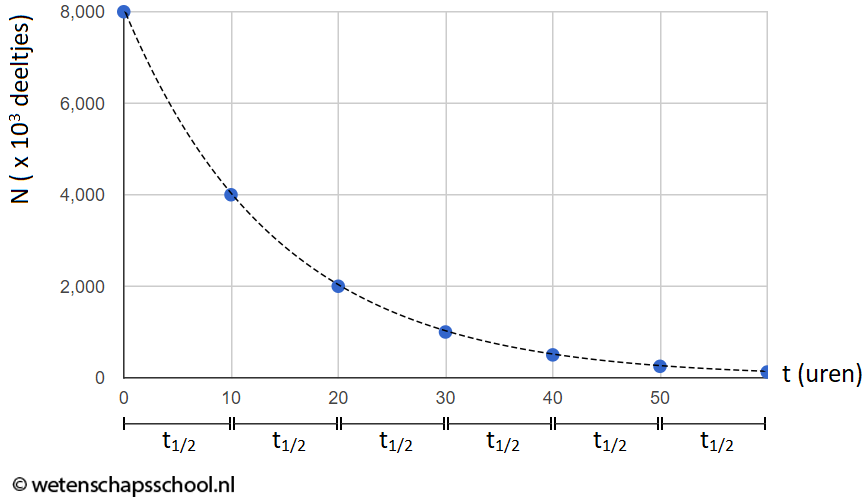
Een vervalkromme is een N,t-diagram, waarin het aantal kernen door de tijd beschreven is. De helling van de grafiek is de activiteit op dat moment. Je kan ook de gemiddelde activiteit berekenen:

\[A_{gem} = \frac{\Delta N}{\Delta t}\]

Uit deze grafiek volgt de volgende formule, waarmee de activiteit van een stof kan worden bepaald gegeven de halveringstijd en het aantal kernen op een specifiek moment:

\[A = \frac{N \cdot \ln(2)}{t_{1/2}}\]

Soorten straling

Soort straling Deeltjes Elektromagnetisch
α β 𝛾
 röntgen
Soort deeltje \(\ce{^4_2He}\) \(\ce{e^-}\) of \(\ce{e^+}\) foton foton
Doordringend vermogen klein
 matig
 groot groot
Ioniserend vermogen groot matig klein klein

Deeltjesstraling

EM-straling

Elektromagnetische straling bestaat uit energiepakketjes genaamd fotonen die met de lichtsnelheid (\(c\)) bewegen. De energie van een foton hangt af van de frequentie (\(f\)) van de straling:

\[E_f = hf\]

Als fotonen door een stof gaan kunnen ze hun energie afgeven en daarmee deeltjes ioniseren. Daarbij verdwijnt het foton. We noemen dit absorptie. Als fotonen door een stof gaan zonder geabsorbeerd te worden noemen we dat transmissie.

De transmissie meten we aan de hand van de intensiteit (\(I\)): de hoeveelheid energie die per m2 wordt doorgelaten. Deze hangt af van de dikte van de stof en het soort materiaal.

De halveringsdikte (\(d_{1/2}\)) is de dikte waarop de intensiteit van de transmissie halveert:

\[I = I_0 \cdot (\frac{1}{2})^{d/d_{1/2}}\]

Bestraling & besmetting

Bij bestraling wordt je blootgesteld aan radioactieve straling. Je wordt er niet zelf radioactief van, maar het is wel schadelijk. Maatregelen:

Bij besmetting komt er een radioactieve stof op of in je lichaam. Daarmee verander jij zelf als het ware in een radioactieve bron. Maatregelen:

(Equivalente) dosis

Het ioniserend vermogen van straling hangt af van:

De dosis (\(D\)) in Gray (Gy) is de hoeveelheid energie die per eenheid lichaamsgewicht wordt geabsorbeerd:

\[D = E_{abs}/m\]

Niet alle soorten zijn even schadelijk, waardoor de dosis soms een slechte indicatie van gevaar of schade kan zijn. Daarom werken we meestal met equivalente dosis (\(H\)) in Sievert (Sv), die corrigeert voor de schadelijkheid van de straling:

\[H = W_R D\]

Waarbij de weegfactor \(W_R = 20\) voor \(\alpha\)-straling, en \(1\) voor alle andere soorten straling.

Achtergrondstraling Soms moet je ook nog corrigeren voor achtergrondstraling uit:

Quantummechanica

Materie heeft massa, lading, energie (\(E_{kin}\) en \(E_{el}\)), en ondervindt krachten.

Straling heeft geen massa, geen lading, wel een ondeelbare hoeveelheid energie, en een constante snelheid (\(c\)). Het ondervindt geen krachten.

In het standaardmodel wordt materie beschouwd als deeltjes en straling als golven. Echter zijn er kenmerken van materie waaruit blijkt dat het ook een golfkarakter vertoont, en andersom ook kenmerken van straling waaruit een deeltjeskarakter volgt.

Quantumdeeltjes vertonen dus zowel golf- als deeltjesgedrag, maar nooit tegelijk. Standaard vertonen deeltjes golfgedrag, maar bij detectie of interactie met andere deeltjes komt het deeltjesgedrag naar voren. Dit verschijnsel noemen we de golf-deeltjesdualiteit.

Dat volgt ook uit het dubbelspleetsexperiment. Daarbij vormen elektronen een interferentiepatroon. Als je een detector plaatst naast één van de spleten, verdwijnt het interferentiepatroon.

Deeltjesgedrag

Kenmerken van deeltjesgedrag zijn:

Deeltjesgedrag van straling

Straling kan worden gezien als een verzameling ‘deeltjes’ of ‘energiepakketjes’, genaamd fotonen. De fotonen dragen de stralingsenergie, die afhangt van de golflengte:

\[E_f = hf = h\frac{c}{\lambda}\]

Bij absorptie of reflectie van fotonen oefenen zij een hele kleine kracht uit. Daarnaast is reflectie een vorm van richtingsverandering. Dit zijn beide kenmerken van deeltjesgedrag.

Foto-elektrisch effect

Fotonen kunnen elektronen vrijmaken uit een metaal. Dat noem je het foto-elektrisch effect. De elektronen komen alleen vrij als de fotonenergie groter dan een minimale drempelwaarde is. Alle overige fotonenergie wordt omgezet in kinetische energie van het elektron.

\[E_f > E_{\text{uittreed}}\] \[E_kin = E_f - E_{\text{uittreed}}\]

Dit experiment bewijst dat straling bestaat uit energiepakketjes. Je zou verwachten dat bij een hogere intensiteit de stralingsenergie wél hoog genoeg zou zijn om elektronen vrij te maken. Echter is de energie verdeeld over meer fotonen, waardoor een individueel foton nog steeds onvoldoende energie heeft om een elektron vrij te maken.

Golfgedrag

Kenmerken van golfgedrag zijn:

Golfgedrag van materie

Als je elektronen door een dubbelspleet schiet ontstaat, net als bij fotonen, een interferentiepatroon. Dit patroon ontstaat ook als de elektronen één voor één afgeschoten worden; het wordt dus niet veroorzaakt door onderlinge botsingen.

De elektronen interfereren dus niet met elkaar, maar met zichzelf. Hieruit volgt dat een individueel elektron door beide spleten tegelijk gaat; het elektron vertoont golfgedrag.

De “golflengte” van het golfkarakter van materie wordt de debrogiegolflengte genoemd, en hangt af van de massa en snelheid van het betreffende deeltje:

\[\lambda = \frac{h}{mv}\]

Het ontstane interferentiepatroon bij elektronen geeft de waarschijnlijkheid aan dat je een elektron aantreft (groot rond de maxima en klein rond de minima).

Gebonden materiedeeltjes

Binnen een atoom kan een elektron zich niet vrij bewegen en is de elektrische energie dus negatief. We zeggen dat het elektron ‘gebonden’ is; om vrij te komen moet je energie toevoeren. We spreken dan ook wel van een energieput.

Energieput van een atoom

In een atoom bevinden elektronen zich in orbitalen rond de atoomkern. In het klassieke model van Bohr zijn dit cirkelvormige banen. In realiteit zijn het driedimensionale staande golven die de waarschijnlijkheid aangeven dat een elektron zich op een willekeurig tijdstip op een plaats bevindt.

Op niveau \(n\) is de baan een staande golf van \(n\) golflengtes.

De orbitalen van een atoom corresponderen met energieniveaus. Een elektron kan naar een hoger energiebaan springen door het absorberen van een foton. De fotonenergie moet dan wel precies gelijk zijn aan het verschil tussen de toestanden.

De energie van een elektron op energieniveau \(n\) van een waterstofatoom bereken je zo:

\[E_n = - \frac{13.6\text{ eV}}{n^2}\]

De totale energie van een elektron binnen een atoom is de som van de elektrische en kinetische energie (\(E_n = E_{kin} + E_{el}\)). Hoe verder van de kern:

Omdat de kinetische energie kleiner is, is de debrogiegolflengte groter in hogere energietoestanden.

Energieput van een molecuul

In een lang molecuul is er niet één kern die de elektronen aantrekt. De elektrische energie is in de lengte richting overal ongeveer even groot. Daardoor kunnen elektronen zich “vrij” bewegen in de lengte van het molecuul.

Daarom gebruiken we een ander model: de oneindig diepe ééndimensionale energieput. We stellen de elektrische energie in het gehele molecuul gelijk aan nul. De enige energie die de elektronen hebben is dus kinetische energie.

Er zijn in een ééndimensionale energieput ook energietoestanden. Die geven niet de afstand tot de kern aan, zoals in een atoom, maar het aantal plaatsen waarop je het elektron kan aantreffen in het molecuul. (Daarom is het ééndimensionaal; alle staande golven lopen door elkaar heen.)

De energieniveaus zijn net als bij een waterstofatoom staande golven die de waarschijnlijkheid aangeven een elektron ergens aan te treffen. Aan de randen van het molecuul zitten knopen. Hoe hoger het energieniveau, hoe kleiner de golflengte, en hoe meer buiken er zijn. Het elektron kan dan op meer plekken in het molecuul zijn.

De energie van een deeltje in energietoestand \(n\) bereken je als:

\[E_n = n^2 \cdot \frac{h^2}{8mL}\] \[E_n = n^2 \cdot E_1\]

Hierbij is \(L\) de lengte van het molecuul (in meters). In de grondtoestand is er één buik, dus \(\lambda_1 = 2L\). Daaruit volgt:

\[L = n \cdot \frac{1}{2} \lambda_n\]

In de ééndimensionale energieput kan elk energieniveau door maar twee elektronen (met tegengestelde spin) bezet worden. Dit noemen we het uitsluitingsprincipe van Pauli.

Dat betekent dat als er een foton is met een golflengte voor een overgang van A naar B, maar energieniveau B is al bezet voor twee elektronen, de foton niet geabsorbeerd wordt.

Verschillen tussen de energieput-modellen

Tunneling

We noemen de energieput van een molecuul oneindig diep omdat de gecombineerde elektrische kracht van alle atomen erg hoog is. Daardoor is er veel kinetische energie nodig om een elektron vrij te krijgen.

In de praktijk is het natuurlijk wel mogelijk om een elektron vrij te krijgen, als je maar genoeg energie blijft toevoeren.

Daarom is de waarschijnlijkheid van het aantreffen van een elektron buiten de randen van het molecuul niet helemaal nul. Er is dus een hele kleine kans dat een elektron daar wel kan zijn.

Als een elekron door die kans uit de energieput ontsnapt, ook al heeft het niet voldoende energie, noem je dat tunneling.

Een voorbeeld daarvan is alfaverval. Bij alfaverval tunnelt een heliumkern door de energiebarriëre die nodig is om de sterke kernkracht (die kerndeeltjes bij elkaar houdt) te overdrempelen. Dit is een toevalsprocess omdat het tunnelen volledig is gebaseerd op kansen (de staande golf geeft kans aan).

Let op! Omdat de golf iets doordring in de wand van de energieput, is de golflengte niet langer gelijk aan \(2L\). Je kan hier dus geen formules van de oneindige energieput gebruiken.

Halfgeleiders

In een metaal delen de atomen hun elektronen. Je kan dit zien als een gigantische energieput met heel veel elektronen; daardoor zijn er heel veel energieniveaus die heel dicht op elkaar liggen.

Omdat de energieniveaus zo dicht op elkaar liggen vormen ze eigenlijk een aaneengesloten energieband, waarbij de elektronenergie niet langer gequantiseerd is. De elektronen kunnen elke mogelijke energie (binnen de band) hebben en ook elke mogelijke energie absorberen of afgeven.

Er zijn twee energiebanden:

Elektronen in de geleidingsband kunnen vrij bewegen en daardoor kan er stroom lopen. De elektronen in de valentieband kunnen dat niet. Om de stof goed te laten geleiden moeten elektronen dus van de valentieband naar de geleidingsband kunnen.

Bij stoffen die goed geleiden overlappen de valentieband en geleidingsband en kunnen elektronen makkelijk overspringen. Daardoor kunnen ze zich afwisselend gedragen als een vrij of gebonden deeltje.

Bij isolatoren is er een band gap (‘verboden gebied’) tussen de twee banden, die zo groot is dat overspringen onmogelijk is. Er kunnen geen elektronen in de geleidingsband komen; er kan geen stroom lopen.

Bij halfgeleiders is de bandgap zo klein (meestal \(\lt1.0\text{ keV}\)). Elektronen kunnen dan uit zichzelf niet overspringen, maar als er extra energie wordt toegevoerd wel. Bijvoorbeeld door:

Als er meer energie wordt toegevoerd kunnen elektronen makkelijker overspringen naar de geleidingsband, en wordt de weerstand van de stof lager (want er gaat makkelijker stroom lopen).

LED

Een LED gaat stroom geleiden als de spanning die je er over zet een minimale drempelwaarde overschrijdt.

Bij het terugvallen van de geleidingsband naar de valentieband wordt er licht uitgezonden. De kleur hangt af van de grootte van het bandgap.

Elektromagnetisme

Een voorwerp heeft heel veel kleine magnetische gebiedjes. Meestal staan die in random richtingen, waardoor ze elkaar opheffen. Als alle magnetische gebiedjes in dezelfde richting staan is er sprake van een magnetisch veld.

Een magneet heeft een noord- en zuidpool. Noord-zuid trekt elkaar aan en noord-noord of zuid-zuid stoten elkaar af. De noordpool geven we doorgaans rood aan, en de zuidpool blauw.

Magneten

Als je een magneet bij een niet-magnetische stof houdt, gaan de gebiedjes in de stof allemaal dezelfde kant op wijzen en wordt de stof (tijdelijk) ook magnetisch.

Dit geldt alleen voor metalen. Moleculaire stoffen hebben geen roosters en ionroosters functioneren anders. Dit is verder geen examenstof.

Soorten

Magnetische velden

Magnetische velden visualiseren de aantrekkende en afstotende werking van magneten aan de hand van veldlijnen.

Een kompasnaald is een kleine magneet die altijd (met zijn noordpool) naar de zuidpool van een andere magneet wijst. Magnetische veldlijnen geven aan in welke richting een kompasnaald zou wijzen op bepaalde punten.

Buiten de magneet lopen de veldlijnen van noord naar zuid; binnen de magneet lopen ze van zuid naar noord.

Hoe dichter de lijnen bij elkaar lopen, hoe sterker de magneet is. De magnetische veldsterkte (\(B\)) bepaalt hoe sterk een magneet aan een andere magneet trekt.

Veldsterkte is een vectorgrootheid. Dat betekent dat als je twee magneten naast elkaar hebt, je hun veldsterktes bij elkaar optelt om de richting van het gecombineerde magneetveld te bepalen.

Aardmagnetisch veld

De aarde heeft een magnetisch veld dat waarschijnlijk wordt veroorzaakt door de ijzeren kern.

De magnetische zuidpool bevindt zich rond de geografische noordpool en andersom. Daarom wijst de noordpool van een kompasnaald in de richting van het geografische noorden.

Elektrische velden

Elektrische velden visualiseren de aantrekkende en afstotende werking van geladen deeltjes, vergelijkbaar met magneetvelden.

De veldlijnen geven aan welke kant een positief geladen deeltje zich op zou bewegen. Je kan ook onthouden dat de veldlijnen van + naar - lopen. In een elektrisch veld hoeven de veldlijnen niet gesloten te zijn. Een elektrisch veld kan dus een monopool hebben:

Als een elektrisch veld geconcentreerd is in een punt (zoals hierboven), noemen we het radiaal. Als de veldlijnen evenwijdig lopen (aka tussen twee platen), noemen we het homogeen.

Hoe dichter de veldlijnen bij elkaar lopen, hoe sterker het elektrisch veld. De elektrische veldsterkte (\(\vec{E}\)) in N/C geeft aan hoe groot de elektrische kracht op een geladen deeltje op dat punt in het veld zou zijn:

\[\vec{E} = F_{el}/q\]

Elektrische kracht & energie

Door de formules voor de elektrische kracht en veldsterkte te combineren kan je de veldsterkte in een punt berekenen, gegeven de afstand \\(r\\) tot het midden van een radiaal elektrisch veld:

\[\vec{E} q = f \frac{q_1q_2}{r^2} \implies \vec{E} = f \frac{q_{\text{veld}}}{r^2}\]

Tot slot is de elektrische energie de arbeid van de elektrische kracht:

\[E_{el} = F_{el} \cdot r = f \frac{q_1q_2}{r} = \vec{E}qr\]

Verschillen tussen magnetische (\(B\)) en elektrische (\(\vec{E}\)) velden

Elektromagneten

Spoel

Als je stroom door een spoel laat lopen wekt die een magnetisch veld op. Boven en onder de spoel liggen de veldlijnen verder uit elkaar, en is het veld dus zwakker.

Voor het magneetveld van een spoel met \(N\) windingen en stroomsterkte \(I\) geldt:

\[B = \mu_0 \cdot \frac{N I}{l_{\text{spoel}}}\]

De waarde van \(\mu_0\) is gegeven.

Stroomdraad

Als je stroom door een rechte stroomdraad laat lopen wekt die ook een magnetisch veld zonder noord- en zuidpool op. De lijnen lopen in oneindige cirkels op een vlak dat loodrecht op de stroomdraad staat.

Hoe verder van de stroomdraad, hoe verder ze uit elkaar liggen, en dus hoe zwakker het magneetveld.

Lorentzkracht

Een lading in een magnetisch veld ondervindt een kracht genaamd de Lorentzkracht (\(F_l\)). Die kracht staat loodrecht op zowel de stroomsterkte (richting waarin positieve deeltjes bewegen) als de veldlijnen.

Als de stroomsterkte en magnetische veldsterkte evenwijdig zijn, is er geen Lorentzkracht.

Elektronen en positronen

De grootte van de Lorentzkracht op een individueel geladen deeltje bereken je als:

\[F_l = Bqv\]

De Lorentzkracht werkt alleen op bewegende deeltjes en staat loodrecht op de snelheid van het deeltje. Daardoor maakt het deeltje een eenparige cirkelbeweging, waarbij geldt:

\[F_l = F_{mpz}\] \[Bqv = \frac{mv^2}{r} \implies Bqr = mv\]

De \(r\) van de cirkelbeweging noemen we de Larmorstraal.

Stroomdraad

De Lorentkracht werkt ook op de stroomdraad als geheel. Je berekent hem dan als:

\[F_l = BIl\]

Loodrechte component

Hierin is B de component van de magnetische veldsterkte die loodrecht op de stroomdraad staat. Stel je hebt dus de volgende situatie:

Je moet dan alleen de loodrechte component van de magnetische veldsterkte nemen. Dit doe je door hem te ontleden, net als een kracht (want het is een vectorgrootheid):

Spoel

In het geval van een spoel met \(N\) bindingen kan je ook de volgende formule gebruiken:

\[F_l = N \cdot BIl\]

Op elke winding oefent zich namelijk een Lorentzkracht uit. Je moet daarom de Lorentzkracht keer het aantal windingen van de spoel doen, om de totale Lorentzkracht op de spoel te berekenen.

Inductie

Inductie is het tegenovergestelde van een elektromagneet. Een elektromagneet wekt een magneetveld op door het laten lopen van stroom. Inductie is andersom: het opwekken van stroom in een spoel met behulp van een magneetveld.

Er gaat stroom lopen bij het veranderen van een magneetveld. We drukken dit uit met de flux. De magnetische flux (\(\phi\)) in Weber (Wb) is het aantal veldlijnen door een oppervlakte:

\[\phi = B_{\bot} A\]

Als de flux groter of kleiner wordt veranderd het magneetveld, en vindt er inductie plaats. De inductiespanning (\(U_{ind}\)) is evenredig met de verandering (aka afgeleide) van de flux. Daaruit volgt de formule:

\[U_{ind} \propto N \cdot \frac{d\phi}{dt}\]

Wet van Lenz

Als je een magneet beweegt en daarmee de flux verandert, reageert de spoel door het opwekken van een meeflux of tegenflux. De spoel wordt dus tijdelijk ook een magneet.

Of het een mee- of tegenflux wordt kan je bepalen aan de hand van de Wet van Lenz:

  1. Bepaal de richting van het uitwendig magneetveld (het magneetveld van de veranderende flux) door de spoel.

  2. Kijk of er een toe- of afname van de flux is. (Beweegt de magneet van de spoel af of er naartoe?)

  3. Bij een toename wordt een tegenflux opgewekt. Het opgewekte magneetveld is dus tegengesteld aan de richting van het uitwendige magneetveld.

  4. Bij een afname wordt een meeflux opgewekt. Het opgewekte magneetveld heeft dus dezelfde richting als het uitwendig magneetveld.

Doordat de spoel een magneet wordt gaat er stroom lopen. De spoel wordt dus een spanningsbron. De richting van de stroom kan je bepalen aan de hand van de rechterhandregel voor spoelen.

Je kan vervolgens bepalen welke kant van de spoel de plus- en minpool wordt. In een spanningsbron loopt de stroom altijd van min naar plus.